pgRouting 模块实践
简介
pgRouting 扩展了 PostGIS/PostgreSQL 地理空间数据库以提供地理空间路由和其他网络分析功能。
该库包含以下功能:
最短路径算法
双向算法
Dijkstra算法的多种应用
距离计算
预备知识
在开始之前,我们会先介绍一下预备的知识,如果你已经对图和图的相关算法有了充足的了解,可以略过此部分。
图的定义
图是由一些点(vertices)和边(edges)组成的。可以分为:
无向图
无向简单图
有向图
有向简单图
有些图的理论中还会包含权重这个概念。可以简单的理解为两点之间的距离。
在 pgRouting 中有几种方式可以表示图:
包含权重的:
(id, source, target, cost)包含双向权重的
(id, source, target, cost, reverse_cost)
其中:
标签 |
含义 |
|---|---|
|
边的标识符,要求是数据库中的一个数据 |
|
边起点的标识符 |
|
边终点的标识符 |
|
从起点到终点的权重(当 cost 是负数时,表示这条边并不存在于图中,同时 cost 在一个查询中必须存在) |
|
从终点到起点的权重(当 reverse_cost 为负数时,表示这条边并不存在于图中) |
图示例
有向图(cost)
SELECT * FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3)) AS t(id, source, target, cost); id | source | target | cost ----+--------+--------+------ 1 | 1 | 2 | 5 2 | 1 | 3 | -3
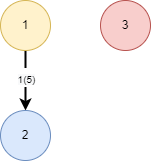
其中 id 为 2 在 cost 为负数,所以在图中没有这个边。
无向图(cost)
SELECT * FROM (VALUES (1, 1, 2, 5), (2, 1, 3, -3)) AS t(id, source, target, cost); id | source | target | cost ----+--------+--------+------ 1 | 1 | 2 | 5 2 | 1 | 3 | -3
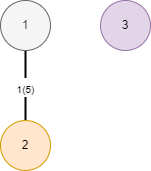
与上面的图相比结点 1 和 节点 2 之间的连线时没有指向的。
有向图(cost, reverse_cost)
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
在上面的示例中,id 为 2(1->3) 和 3(3->2)
的两条边就是不存在的,因为cost 和 reverse_cost 是负数。
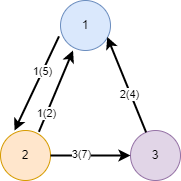
无向图(cost, reverse_cost)
SELECT *
FROM (VALUES (1, 1, 2, 5, 2), (2, 1, 3, -3, 4), (3, 2, 3, 7, -1))
AS t(id, source, target, cost, reverse_cost);
id | source | target | cost | reverse_cost
----+--------+--------+------+--------------
1 | 1 | 2 | 5 | 2
2 | 1 | 3 | -3 | 4
3 | 2 | 3 | 7 | -1
(3 rows)
在上面的示例中,id 为 2(1–3) 和 3(3–2) 的边是不存在的,因为 cost
或 revrese_cost 为负数。
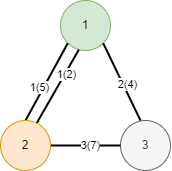
不使用 geometry 的图
人际关系,基因,文件依赖等问题都可以通过 pgRouting 来解决,这些问题一般都不需要 geometry 数据。现在我们使用 Wiki 上的一个示例来进行说明:

其中:
找到从结点 1 到结点 5 的最短路径
是一个无向图
有 6 个结点
有 9 条边
创建一个 pgroutetest 数据库 ,并创建扩展
CREATE DATABASE pgroutetest; -- 连接到 pgroutetest 数据库 \c pgroutetest CREATE EXTENSION pgRouting CASCADE;
创建表,字段如下:
CREATE TABLE wiki ( id SERIAL, source INTEGER, target INTEGER, cost INTEGER );
插入数据
INSERT INTO wiki (source, target, cost) VALUES (1, 2, 7), (1, 3, 9), (1, 6, 14), (2, 3, 10), (2, 4, 15), (3, 6, 2), (3, 4, 11), (4, 5, 6), (5, 6, 9);
寻找最短路径
为了解决这个问题我们使用了 Dijkstra 算法。
SELECT * FROM pgr_dijkstra( 'SELECT id, source, target, cost FROM wiki', 1, 5, false); seq | path_seq | node | edge | cost | agg_cost -----+----------+------+------+------+---------- 1 | 1 | 1 | 2 | 9 | 0 2 | 2 | 3 | 6 | 2 | 9 3 | 3 | 6 | 9 | 9 | 11 4 | 4 | 5 | -1 | 0 | 20
即最短路径为 1->3->6->5
查看边的信息
SELECT id, in_edges, out_edges FROM pgr_extractVertices('SELECT id, source, target FROM wiki'); id | in_edges | out_edges ----+----------+----------- 3 | {2,4} | {6,7} 5 | {8} | {9} 4 | {5,7} | {8} 2 | {1} | {4,5} 1 | | {1,2,3} 6 | {3,6,9} |
使用 Geometry 的图
创建一个数据库
createdb sampledata psql sampledata -c "CREATE EXTENSION pgrouting CASCADE"
导入数据
这里我们手动导入数据,当然,你可以使用其他工具来导入数据,例如:
shp2pgsql
ogr2ogr
osm2pgsql
osm2pgrouting
下图是一个整体的图说明:
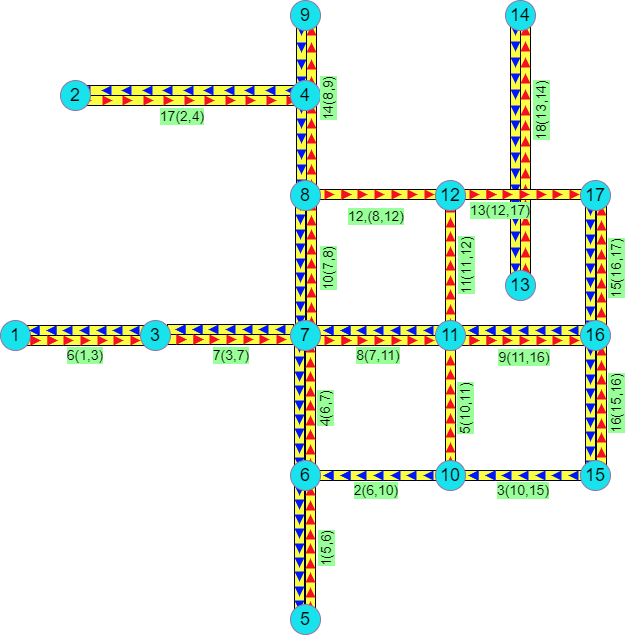
边
在数据库的设计中有一些字段会包含一个
reverse_的前缀来表示相反的方向。字段
说明
id唯一标识符
source起始顶点标符
target结束顶点标识符
cost从起点到终点的成本(权重)
capacity从起点到终点的流量
reverse_cost从终点到起点的成本(权重)
reverse_capacity从终点到起点的流量
x1起始点 x 坐标
y1起始点 y 坐标
x2终止点 x 坐标
y2终止点 y 坐标
geom边的 geometry 数据
创建边的表:
CREATE TABLE edges ( id BIGSERIAL PRIMARY KEY, source BIGINT, target BIGINT, cost FLOAT, reverse_cost FLOAT, capacity BIGINT, reverse_capacity BIGINT, x1 FLOAT, y1 FLOAT, x2 FLOAT, y2 FLOAT, geom geometry );
插入数据:
INSERT INTO edges (cost, reverse_cost, capacity, reverse_capacity, geom)
VALUES (1, 1, 80, 130, ST_MakeLine(ST_POINT(2, 0), ST_POINT(2, 1))),
(-1, 1, -1, 100, ST_MakeLine(ST_POINT(2, 1), ST_POINT(3, 1))),
(-1, 1, -1, 130, ST_MakeLine(ST_POINT(3, 1), ST_POINT(4, 1))),
(1, 1, 100, 50, ST_MakeLine(ST_POINT(2, 1), ST_POINT(2, 2))),
(1, -1, 130, -1, ST_MakeLine(ST_POINT(3, 1), ST_POINT(3, 2))),
(1, 1, 50, 100, ST_MakeLine(ST_POINT(0, 2), ST_POINT(1, 2))),
(1, 1, 50, 130, ST_MakeLine(ST_POINT(1, 2), ST_POINT(2, 2))),
(1, 1, 100, 130, ST_MakeLine(ST_POINT(2, 2), ST_POINT(3, 2))),
(1, 1, 130, 80, ST_MakeLine(ST_POINT(3, 2), ST_POINT(4, 2))),
(1, 1, 130, 50, ST_MakeLine(ST_POINT(2, 2), ST_POINT(2, 3))),
(1, -1, 130, -1, ST_MakeLine(ST_POINT(3, 2), ST_POINT(3, 3))),
(1, -1, 100, -1, ST_MakeLine(ST_POINT(2, 3), ST_POINT(3, 3))),
(1, -1, 100, -1, ST_MakeLine(ST_POINT(3, 3), ST_POINT(4, 3))),
(1, 1, 80, 130, ST_MakeLine(ST_POINT(2, 3), ST_POINT(2, 4))),
(1, 1, 80, 50, ST_MakeLine(ST_POINT(4, 2), ST_POINT(4, 3))),
(1, 1, 80, 80, ST_MakeLine(ST_POINT(4, 1), ST_POINT(4, 2))),
(1, 1, 130, 100, ST_MakeLine(ST_POINT(0.5, 3.5), ST_POINT(1.999999999999, 3.5))),
(1, 1, 50, 130, ST_MakeLine(ST_POINT(3.5, 2.3), ST_POINT(3.5, 4)));
在 QGIS 中我们就可以看到插入的数据了
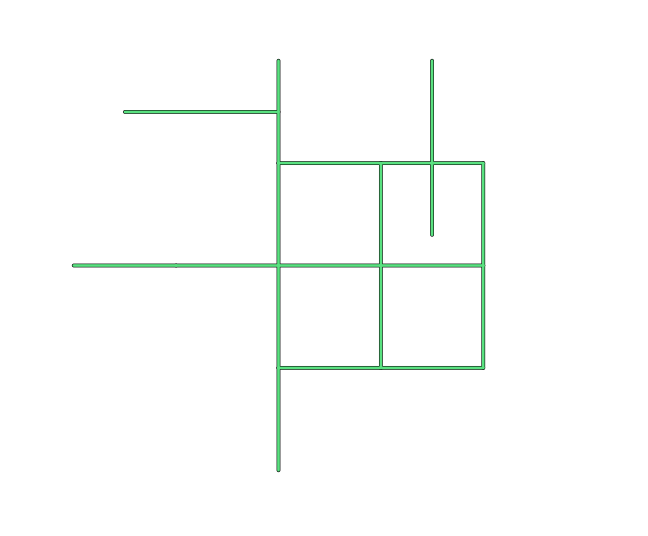
顶点
现在我们已经有了边的数据,我们就可以使用
pgr_extractVertices函数将顶点信息保存在一个数据表中SELECT * INTO vertices FROM pgr_extractVertices('SELECT id, geom FROM edges ORDER BY id');
现在,我们查看一下顶点的数据:
SELECT * FROM vertices; id | in_edges | out_edges | x | y | geom ----+----------+-----------+----------------+-----+-------------------------------------------- 1 | | {6} | 0 | 2 | 010100000000000000000000000000000000000040 2 | | {17} | 0.5 | 3.5 | 0101000000000000000000E03F0000000000000C40 3 | {6} | {7} | 1 | 2 | 0101000000000000000000F03F0000000000000040 4 | {17} | | 1.999999999999 | 3.5 | 010100000068EEFFFFFFFFFF3F0000000000000C40 5 | | {1} | 2 | 0 | 010100000000000000000000400000000000000000 6 | {1} | {2,4} | 2 | 1 | 01010000000000000000000040000000000000F03F 7 | {4,7} | {8,10} | 2 | 2 | 010100000000000000000000400000000000000040 8 | {10} | {12,14} | 2 | 3 | 010100000000000000000000400000000000000840 9 | {14} | | 2 | 4 | 010100000000000000000000400000000000001040 10 | {2} | {3,5} | 3 | 1 | 01010000000000000000000840000000000000F03F 11 | {5,8} | {9,11} | 3 | 2 | 010100000000000000000008400000000000000040 12 | {11,12} | {13} | 3 | 3 | 010100000000000000000008400000000000000840 13 | | {18} | 3.5 | 2.3 | 01010000000000000000000C406666666666660240 14 | {18} | | 3.5 | 4 | 01010000000000000000000C400000000000001040 15 | {3} | {16} | 4 | 1 | 01010000000000000000001040000000000000F03F 16 | {9,16} | {15} | 4 | 2 | 010100000000000000000010400000000000000040 17 | {13,15} | | 4 | 3 | 010100000000000000000010400000000000000840 (17 rows)
在数据我们可以看到 id 为 3 的顶点有进入为 6 的边,出去为 7 的边。
拓扑
现在我们就可以设置边表中起始点和终止点的 id。
/* -- 设置起点信息 */ UPDATE edges AS e SET source = v.id, x1 = x, y1 = y FROM vertices AS v WHERE ST_StartPoint(e.geom) = v.geom; /* -- 设置终点信息 */ UPDATE edges AS e SET target = v.id, x2 = x, y2 = y FROM vertices AS v WHERE ST_EndPoint(e.geom) = v.geom;
查看一下拓扑数据:
SELECT id, source, target FROM edges ORDER BY id; id | source | target ----+--------+-------- 1 | 5 | 6 2 | 6 | 10 3 | 10 | 15 4 | 6 | 7 5 | 10 | 11 6 | 1 | 3 7 | 3 | 7 8 | 7 | 11 9 | 11 | 16 10 | 7 | 8 11 | 11 | 12 12 | 8 | 12 13 | 12 | 17 14 | 8 | 9 15 | 16 | 17 16 | 15 | 16 17 | 2 | 4 18 | 13 | 14
我们可以在 QGIS 中查看当前的点和边: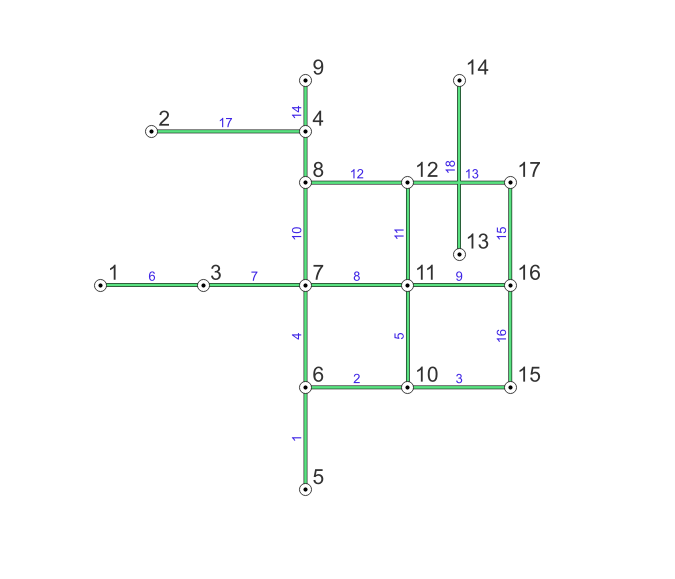
这里我们可以看到 id 为 1 的边的起始点为 5,终止点为 6。
API 说明
API 具体说明可参考官方文档。
本文档参考pgRouting官方文档。